第 11 章 部分計分模型: 第一部分
在本課程中,我們將學到
- 部分計分模型(Partial Credit Models)的正式規範與參數的處理
- 參數的估計
- 參數的詮釋
- 部分計分模型的試題特徵曲線(ICCs)
- 在 R 環境中將數據重新編碼
當測驗題目需要用0分、1分與2分等方式進行部分計分,而不僅只考量題目作答是正確或錯誤,適合用來分析這樣評分結果的模型稱之為部分計分模型(partial credit model, PCM),或是多元計分模型,藉以與二元計分模型做區分。二元計分模型是部分計分模型的一個特例,在本課中關於部分計分的說明都可以應用於二元計分模型。
11.1 使用部分計分模型的優點
如果我們能夠把學生對題目的作答反應分成不只兩個類別(即正確或錯誤),我們將可以獲得更多關於學生作答這些題目的資訊。例如,如果有一群學生答對或答錯某一道題目,與其就說該組學生可能是高能力者或低能力者,我們倒不如根據學生不同程度的作答反應,透過部份計分的方式,辨別出那些部份答對者,並視他們可能為中間能力的學生。如果我們有更多道部分計分的題目,則整個測驗卷就可以根據學生的作答結果,更可靠地把學生區分成不同的能力群。換句話說,一個測驗能夠將學生分成多少個得分類別(total number of score points),會與該測驗的信度有直接的關係。
然而,並非每道題目都適合進行部分計分。某些題目按照其性質只能有正確或錯誤的答案,例如是非題。而有些題目我們會發現,有些低能力學生可能會答錯題目,但有些卻能部分答對。一般而言,當我們以部分給分的方式進行評分,我們需要確認獲得比較高分的學生,他們的確是能力比較強的學生。在下一課中,我們會討論多元計分題目的評分準則。
11.2 部分計分模型的數學參數形式
對於二元計分模型(3.1)而言,答對某一題的機率是取決於學生的能力參數與該題的題目難度參數。至於用0分、1分與2分等方式來評分的多元計分題目,其部分計分模型會牽涉到兩個題目難度參數,以及一個學生能力參數,如下列公式所示:
\[\begin{equation} Prob(X=0) = \frac{1}{1+\exp(\theta - \delta_1)+\exp(2\theta - \delta_1- \delta_2))} \\ \end{equation}\] \[\begin{equation} Prob(X=1) = \frac{\exp(\theta - \delta_1)}{1+\exp(\theta - \delta_1)+\exp(2\theta - \delta_1- \delta_2)} \\ \end{equation}\] \[\begin{equation} Prob(X=2) = \frac{\exp(2\theta - \delta_1- \delta_2)}{1+\exp(\theta - \delta_1)+\exp(2\theta - \delta_1- \delta_2)}\tag{11.1} \end{equation}\]
其中 \(\theta\) 是能力參數,而 \(\delta_1\) 和 \(\delta_2\) 是該題的兩個難度參數。請注意,上述三個式子的分母皆相同,而且它等於三個式子的分子加總,這使得在該題得到0分、1分或2分的機率相加就會等於1。
11.3 PCM 題目難度參數的詮釋
在二元計分的情況下,題目難度參數 \(\delta\) 反映具有該能力值的學生,他們有50%的機會答對該題。換句話說,當一位學生的能力值等於某一題的難度時,則這位學生在該題獲得0分或1分的機會是相等的。
同理,對於部分計分模型而言,當某些學生的能力等於其中一個 \(\delta\) 值時,該等學生將會有同樣的機會獲得兩個相連分數的其中一個,例如那些能力為 \(\delta_1\) 的學生,他們會有相同的機會獲得0分或1分,而那些能力為 \(\delta_2\) 的學生,他們會有相同的機會獲得1分或2分。由於多元計分會有超過兩個得分的類別,僅知道學生有同樣的機會落在兩個相連得分類別的其中一個,並不能夠告訴我們關於該題難度的所有資訊。以下我們以圖示的方式呈現 \(\delta\) 值的位置,該圖可以讓我們探討\(\delta\)的詮釋。
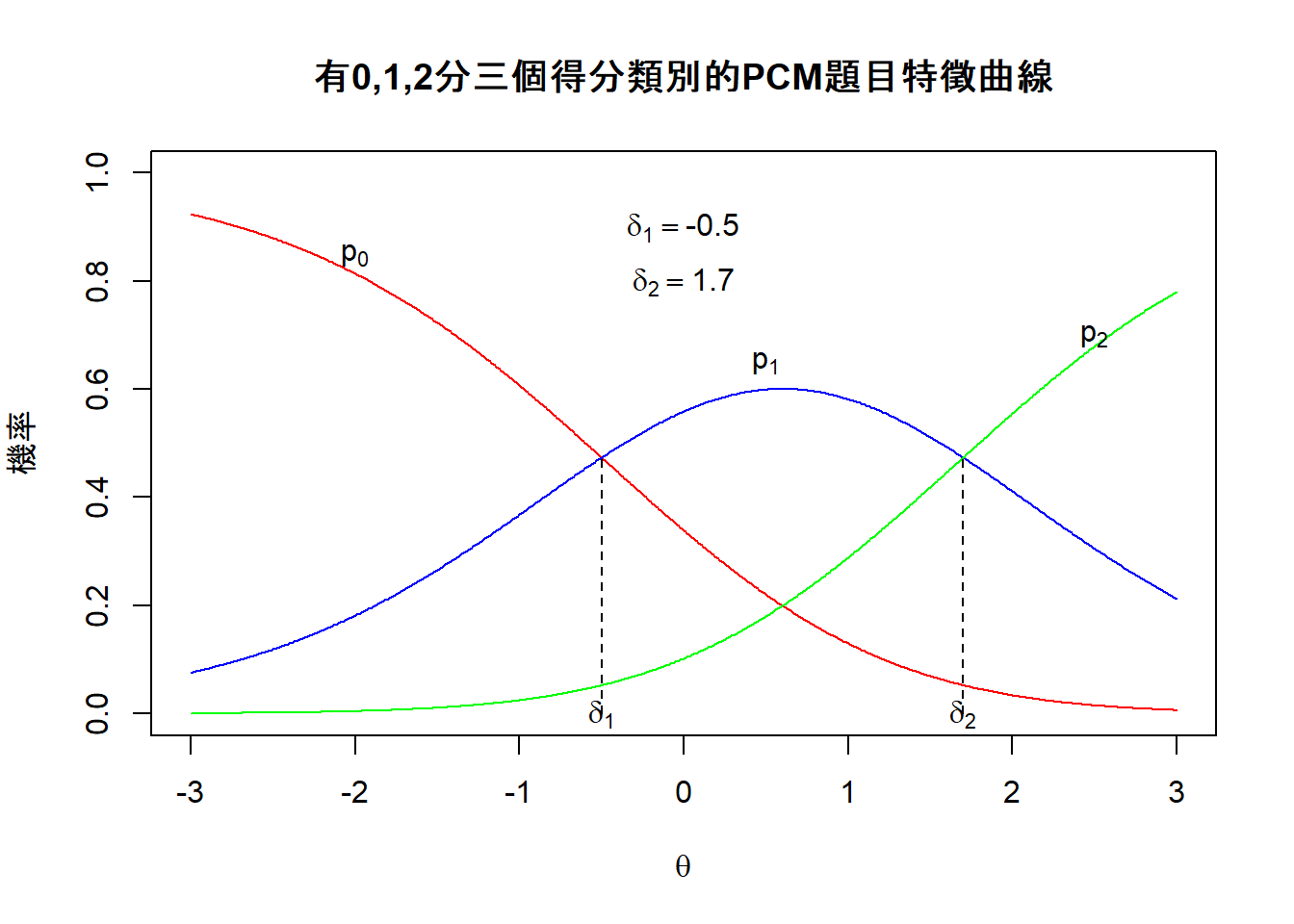
图 11.1: deltas為順序的PCM題目特徵曲線
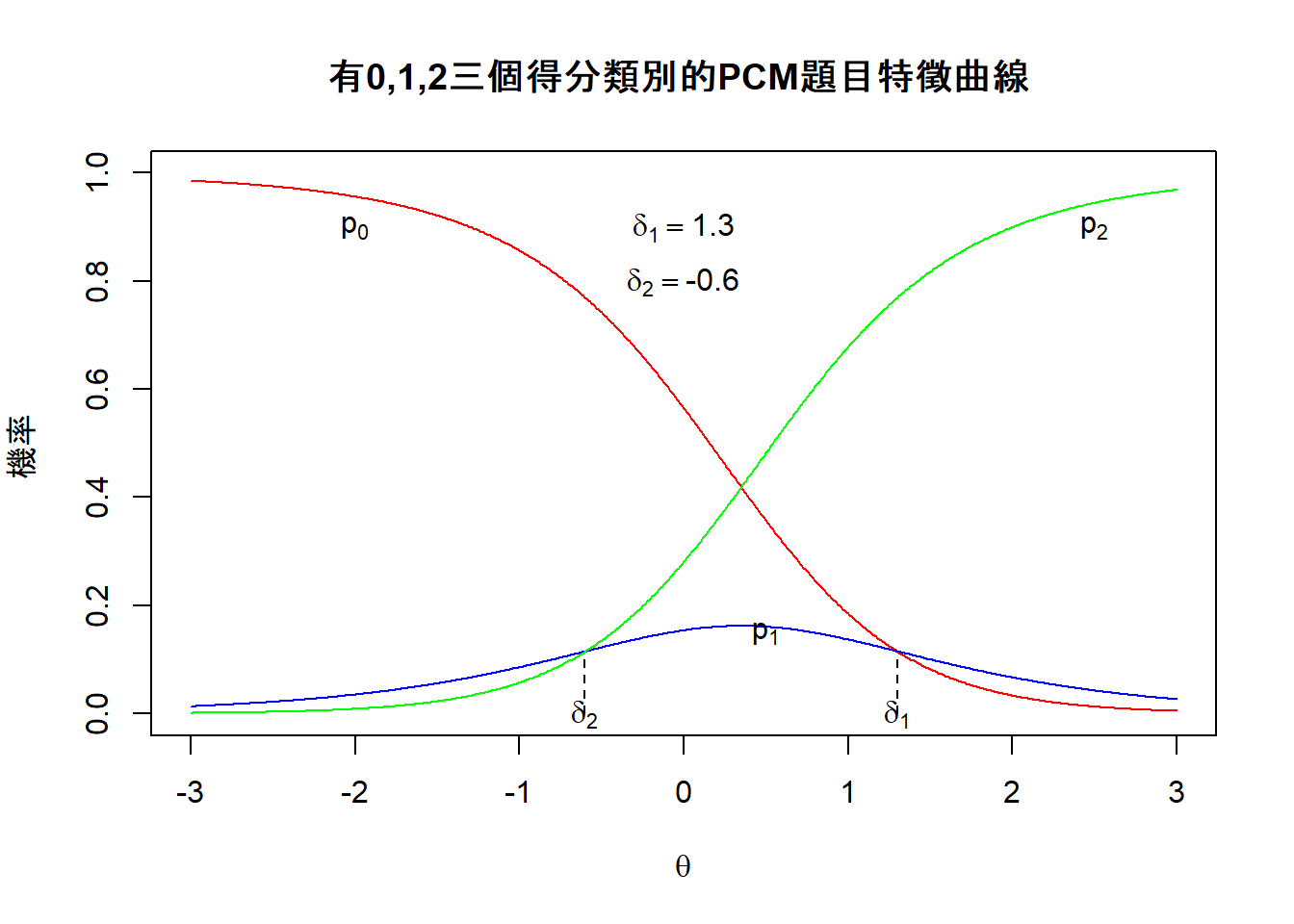
图 11.2: deltas為非順序的PCM題目特徵曲線
圖 11.1和圖 11.2呈現兩個多元計分題目的題目特徵曲線,它們是按照 Eq.(11.1) 的計算後繪製而成。
從上述兩個圖中可見,\(\delta_1\) 是\(p_0\) 和 \(p_1\) 兩條曲線的交叉點,它代表在該能力值的學生獲得0分或1分的機率剛好相等。\(\delta_2\) 是 \(p_1\) 和 \(p_2\) 兩條曲線的交叉點,它代表在該能力值的學生獲得1分或2分的機率剛好相等。然而,在圖11.1中,我們可以觀察到 \(\delta_1\) 的值是小於 \(\delta_2\) 的值,而在圖11.2中,我們可以觀察到 \(\delta_1\) 的值是大於 \(\delta_2\) 的值,此現象稱之為非順序的閾值(disordered thresholds),非順序的閾值的出現通常是因為得到中間分數(在此例子中是指得1分者)的學生人數非常少,這反映在圖中的 \(p_1\) 曲線特別低。非順序閾值的出現並非反映出該題是有問題的題目,此現象的出現只不過是反映大部份學生不是得到0分就是2分,很少學生得到1分而已。
當我們看到類似圖11.2中幾個\(\delta\)並非順序時,此時要詮釋這些\(\delta\) 值就沒有那麼單純了。很多時候,該等\(\delta\)並不適合詮釋為該題的難度層級(step difficulties),因為它們只反映局部的(或條件的) 情況,即\(\delta\)值反映兩個相連得分類別的機率相等,而沒有考慮其他得分類別的機率。在學術界,關於難度層級的詮釋是頗具爭議。
11.4 Thurstonian閾值
其中一種處理PCM 題目層級難度的方法是使用Thurstonian閾值的概念,Thurstonian閾值是指一個能力值,具有該能力值的學生會有50%的機會獲得某一個分數或比此分數更高的分數。例如,假設某一題的得分為0或1或2分,則第一個Thurstonian閾值 \(\gamma_1\) 是指具有 \(\gamma_1\) 能力值的學生,他們會有50%的機會獲得1或2分,如下公式所示:
\[\begin{equation} Prob(X=1 \text{ or } 2/\theta=\gamma_1) = 0.5 \end{equation}\]
在上述例子的圖11.1與11.2中,其Thurstonian閾值所相對應的位置用圖11.3與圖11.4來呈現出來。
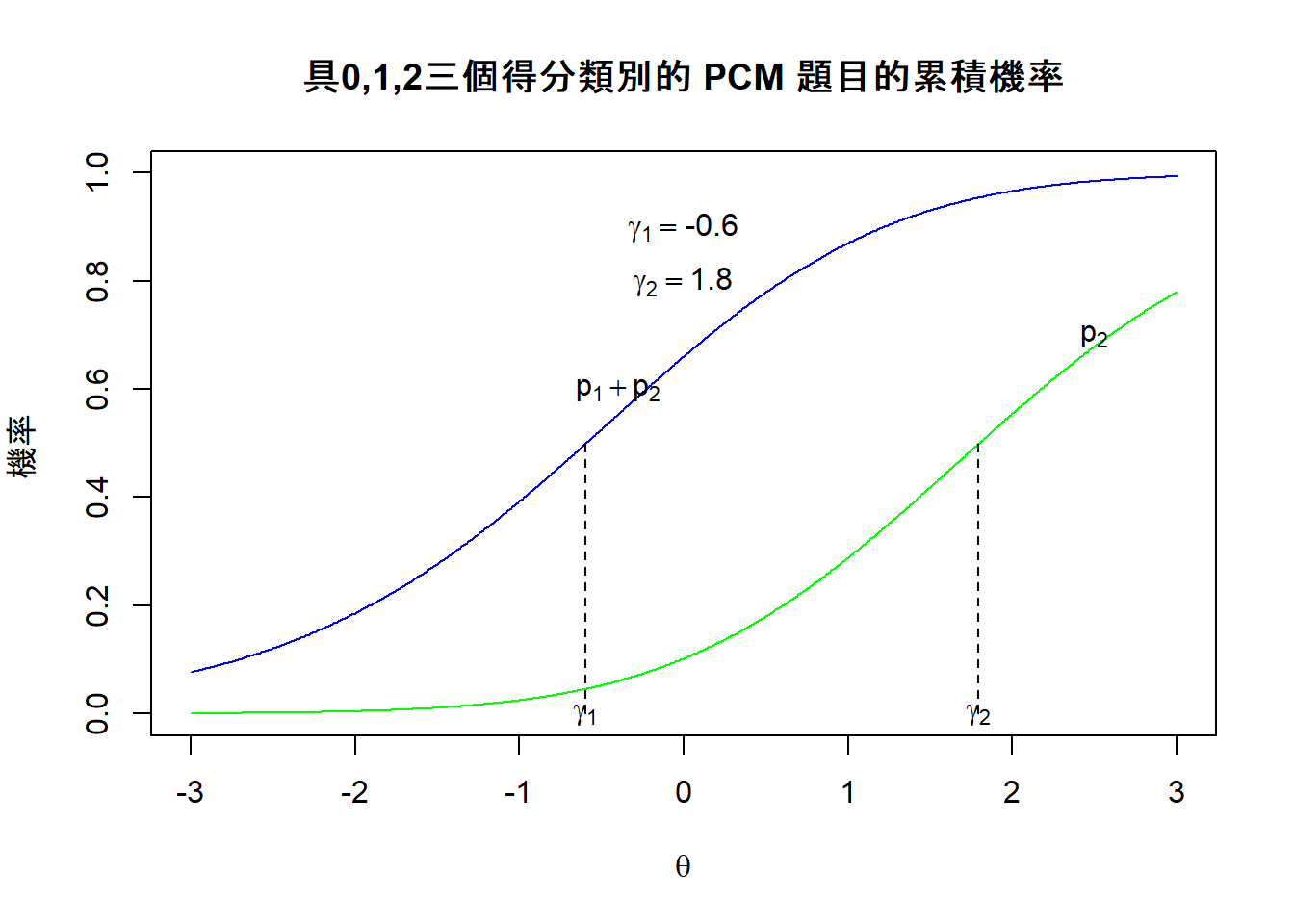
图 11.3: Thurstonian閾值範例1
在圖11.3中,\(\gamma_1\) (= -0.6) 是指具有該能力的學生,他們有50%的機會得到1分或2分,其實也可以說是他們起碼得到1分,而\(\gamma_2\) (= 1.8)是指具有該能力的學生,他們有50%的機會得到2分,其實也可以說是起碼得到2分,但在此例子中,2分已經是最高分。如果我們比較deltas 與 gammas的值,其中\(\delta_1=\) -0.5 、 \(\delta_2=\) 1.7 與 \(\gamma_1=\) -0.6 、 \(\gamma_2=\) 1.8 ,我們可以發現deltas 與 gammas之間的值差異沒有很大。
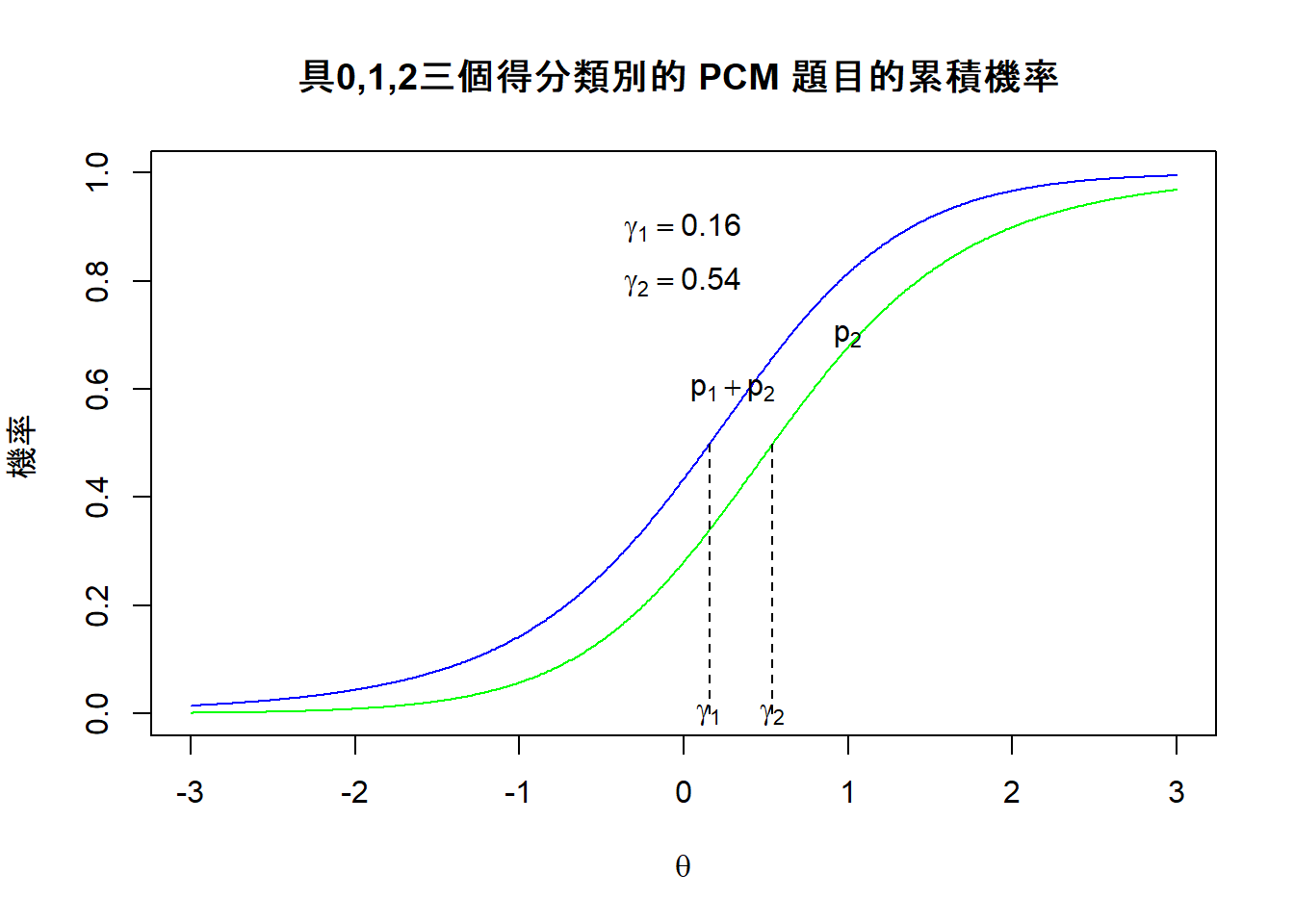
图 11.4: Thurstonian閾值範例2
在圖11.4中, \(\gamma_1\) (= 0.16) 是指具有該能力的學生,他們有50%的機會獲得1分或2分(另一個說法是起碼得到1分),而能力值為\(\gamma_2\) (= 0.54) 的學生,他們有50%的機會獲得2分。如果我們將deltas 與 gammas 值做一個比較,我們將\(\delta_1=\) 1.3 、 \(\delta_2=\) -0.6 與 \(\gamma_1=\) 0.16 、 \(\gamma_2=\) 0.54 的值相比,這一次我們發現 deltas 與 gammas的值差別比較大,其實 \(\gamma_1\) 與 \(\gamma_2\) 的值很接近,代表獲得1分的人很少,這是因為獲得起碼1分的機率與獲得2分的機率非常接近,這一點可以從觀察到\(p_1+p_2\)的曲線與\(p_2\)的曲線很接近而反映出來。
11.5 期望得分曲線
我們將以另外一個途徑來了解 PCM 題目每一個得分值所對應的題目難度,方法是透過建立以期望得分(expected score)作為能力值的函數,接著就可以透過該函數找出哪些能力值會分別對應到0、1或2等等的期望得分。
例如,圖11.5呈現本例題的期望得分曲線,如下所示。
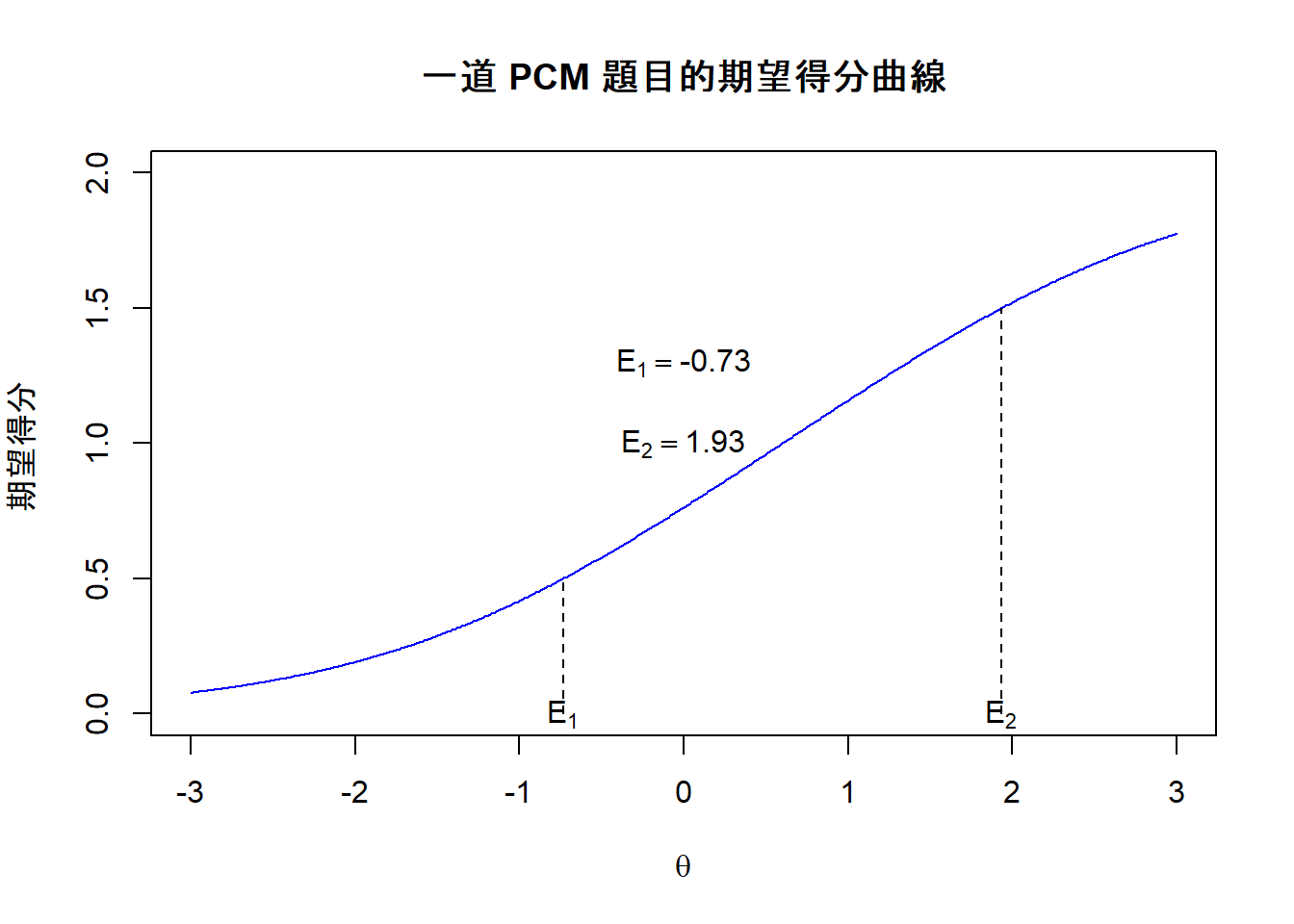
图 11.5: 期望得分曲線範例1
當學生的能力值是介於-0.73 與 1.93 之間,則它們的期望得分會介於0.5與1.5之間,我們可以稱這個能力區間為得1分的區間。當學生的能力值是低於-0.73時,他們的期望得分比較接近0分而不是1分,因此這個區域可以稱之為得0分的區域。至於那些能力超過1.93 的學生,他們的期望得分會比較接近2分而非1分,因此我們可以稱此區域為得2分的區域。在這個架構之下,-0.73 與 1.93可以視為是該道PCM題目的難度值。綜上所述,我們共有3套具潛力而且可以視為是PCM題目的難度值,即\(\delta_1=\) -0.5, \(\delta_2=\) 1.7 、\(\gamma_1=\) -0.6 、 \(\gamma_2=\) 1.8 與 \(E_1=\) -0.73 、 \(E_2=\) 1.93。
11.6 應用部分得分模型來進行校準的 R 程式碼範例
由於二元計分模型是多元計分模型的一個特例,因此用PCM 進行校準與用二元計分模型進行校準的方法是一致的,本書前面的章節對二元計分模型已經有所介紹。接下來的例子,我們所用的資料是一個調查對電腦熟識程度的問卷,該資料集可在此下載 。
該資料集是以文字檔的形式來建立,編碼皆以A、B、C與D來呈現。我們透過以下的 R 程式碼來讀進文字檔,並將資料進行轉碼,接著還會繪製 PCM 的題目特徵曲線(ICC’s)與能力和難度對應圖(Wright Map)。 、
rm(list=ls())
library(TAM)
library(WrightMap)
setwd("C:/G_MWU/ARC/Philippinesfiles") #將你的目標資料夾設為工作目錄
resp <- read.fwf("ComputerSurvey.dat", widths=c(rep(1,26)), stringsAsFactors = FALSE)
colnames(resp) <- paste0("Q",seq(1,ncol(resp)))
# 將A、B、C與D轉換成為0、1、2與3,並將 NA 設為遺漏值。
resp[resp=="A"] <- 0
resp[resp=="B"] <- 1
resp[resp=="C"] <- 2
resp[resp=="D"] <- 3
resp[resp=="Z"] <- NA
# 將原始資料改變成為數據形式的資料(numeric type)
resp <- sapply(resp, as.numeric)
# 找出所有交空白卷的人(即完全沒有作答者)
d <- apply(resp,1,function(x){all(is.na(x))})
# 移除該等完全沒有作答者
resp <- resp[-which(d),]
mod1 <- tam.jml(resp)
thres <- tam.threshold(mod1) # 求出Thurstonian閾值
wrightMap(mod1$WLE, thres, item.side = itemClassic)
wrightMap(mod1$WLE, thres) # 嘗試不同方式呈現能力和難度對應圖(Wright Map)
plot(mod1) # 繪製期望得分曲線
plot(mod1,type="items") # 繪製題目特徵曲線
mod1$item1 # 報導題目參數(deltas)11.7 練習題
這裡有一組20道PCM題目的資料檔,每道題目有三種得分,分別為0、1、2分,可由 此下載 。請用PCM模型對該組資料進行校準,並繪製題目特徵曲線與能力和難度對應圖。你發現哪些題目是最困難的?哪些題目是最簡單的?