第 4 章 估計 Rasch 模型參數
本節課將會著重於如何實際操作 R 軟體來估計 Rasch 模型。
4.1 練習1
在TAM 套件中,運用下列的 R 編碼來分析 data.sim.rasch 的資料集 。
rm(list=ls()) #清除在 R 環境中所有變數
library(TAM) #讀取 TAM 套件讓我們可以運用套件中的功能
#首先,應用TAM 套件來分析 data.sim.rasch 的資料集
data("data.sim.rasch") # 打開資料集讓我們可以使用它
head(data.sim.rasch) # 可以觀察資料集中的內容
# 應用聯合最大概似估計法(Joint Maximum Likelihood Estimation, JMLE)來估計 Rasch 模型的參數
mod1 <- tam.jml(data.sim.rasch)
#所有 Rasch 分析的結果將會儲存於名為"mod1"的物件
summary(mod1) #可以檢查分析結果的摘要
#可以檢查 Rasch 分析的個別結果
mod1$item
mod1$WLE
mod1$WLEreliability
#你可以輸出題目及能力參數的統計摘要資訊
summary(mod1$item1)
summary(mod1$WLE)
hist(mod1$WLE)
#你可以畫出題目特徵曲線
plot(mod1)關於輸出題目特徵曲線的備註
如果你在輸出題目特徵曲線到檔案時遇到問題,你可以嘗試使用下列兩種方法。 第一,你可以將它們輸入到一個pdf檔案中,例如:
pdf("ICCplots.pdf")
plot(mod1)
dev.off()我有時候需要執行 dev.off() 指令兩次,否則所有輸出會存成一個pdf檔。我有時候必須要執行 dev.new(RStudioGD) 指令來確保圖形能在 RStudio 中呈現。你可以用 dev.cur() 指令來確定現在正在使用的是哪一個圖形呈現方式(graphic device, 如視窗)。目前我對於 R 圖形呈現方式的瞭解還不是很足夠。
第二,如果你沒辦法順利輸出題目特徵曲線,你可以使用下列的編碼來將它們逐一輸出:
for (i in 1:mod1$nitems){
plot(mod1,items=i)
} 每一個圖中會繪製出兩條題目特徵曲線,其中藍色平滑的曲線是按照 Rasch 理論 (3.1)所推導出來的理論機率值而繪製的試題特徵曲線,至於黑色線條是由六個點連結起來,它代表從觀察資料繪製出來的試題特徵曲線。由於 data.sim.rasch 的資料集是從Rasch 模型理論直接模擬出來的,因此這兩條試題特徵曲線非常接近。
4.2 繪製學生能力與試題難度對應圖(Wright Map)
能力與難度對應圖(Wright Map)是一個非常有用的圖形,它將能力估計值的分布與題目的位置放在同一個圖型上,因此亦可稱它為題目與受試者關係圖(Item-person map)。我們可以應用 WrightMap 套件 (Irribarra and Freund 2014) 來繪製,但請先確認你是否已經安裝 WrightMap 套件。
library(WrightMap)
wrightMap(mod1$WLE, mod1$xsi, item.side = itemClassic)能力與難度對應圖(Wright Map)會顯示在 4.1 圖中。
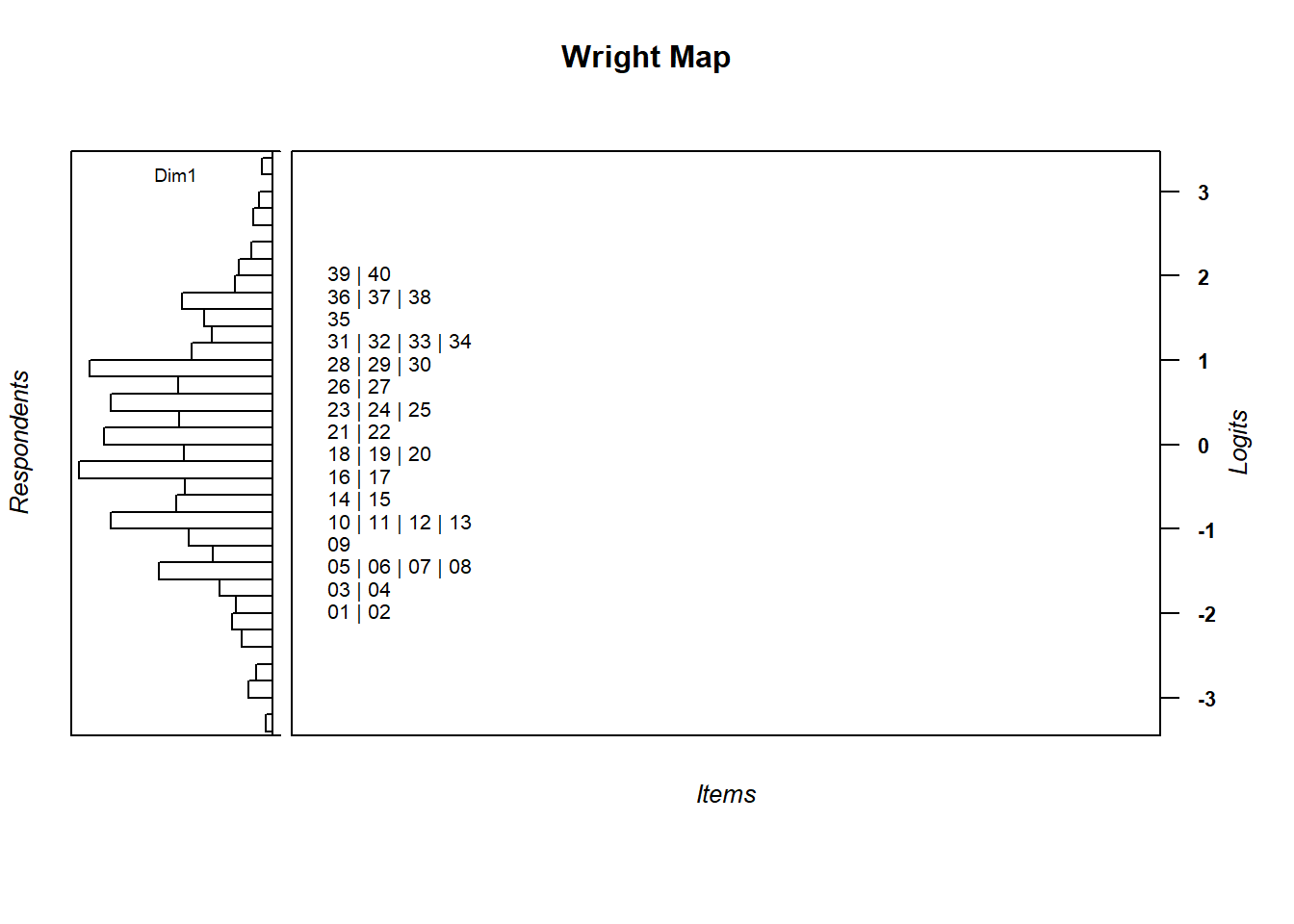
图 4.1: Wright Map
4.1 圖的左側呈現學生能力值的分布,而右側呈現題目的位置及題號。由於用電腦產生模擬資料時,題目的難度是從第1題遞增到第40題,題目難度是題號越後面、難度越難,而且這也反映在能力與難度對應圖(Wright Map)中,第1題與第2題是最簡單的題目,而第39題與第40題是最困難的題目。同理,能力分布最下面的點代表能力較低學生的能力值,而高能力的學生他們都位於分布的上方。再次強調,題目的難度是透過能力量尺來定義,因此我們可以直接指出學生答對某一題的機率。但在古典測驗理論的架構下,我們無法畫出這一類的圖形,因為題目難度與學生能力值無法直接進行比較。
4.3 練習 2
請使用 CTT 套件中的 CTTdata 資料集,並進行題目反應理論的分析。可是當要執行 tam.jml 的功能前,要先將原始資料進行評分的動作。
請比較題目反應理論(IRT)的題目難度估計值與在古典測驗理論(CTT)所估計出的題目得分。
請用 R 軟體中的 cor 功能來計算兩者的線性相關係數,並執行 plot 功能來畫出這兩個變數的分散圖。
請比較題目反應理論與古典測驗理論的信度係數資訊。
請透過視覺觀察題目反應理論試題特徵曲線的斜率以及古典測驗理論點二系列相關係數值的關係。
請比較題目反應理論的能力估計值(WLE) 與古典測驗理論所估計的學生得分。
請計算這兩種估計值的線性相關係數,並透過分散圖呈現這兩者之間的關係。