第 12 章 部分計分模型 - 第二部分
在本節課中,我們將學到
- 對多元計分題目評分時,需要考慮的事項
- 部分計分模型與雙參數模型的比較
12.1 每題的最高配分
我們經常會看到,在一個測驗中,老師設定不同題目的最高配分並不相同,例如,某一道題目的最高配分設為5分,而另外一道題目的最高配分則設為2分。想想看,有什麼因素可以用來決定一道題目最高配分應該為幾分?我們曾經詢問一些命題者,他們是根據什麼判准來決定某一題該配多少分為滿分?我們通常得到如下的回應: “這視乎題目的難度而定”,又或者是”這視乎學生需要多少作答時間來回答這一題”。有些時候,命題者會檢查該題的答案可以區分為多少個步驟或者是部分,然後決定該題應該配多少分。
我們必須說明的是,一道題目的配分並不是根據題目的難度而定,這一點尤其與選擇題有關。對於一道困難的題目,學生常會透過猜測來作答,因此獲得正確答案與其說是因為學生具有高能力,更有可能是因為運氣的因素。
以下我們將討論一些與題目配分有關的因素。
12.2 題目權重、題目資訊和題目鑑別度
假設第一題最高的配分為5分,第二題最高的配分為1分,則對整個測驗的得分而言,第一題配分的權重是第二題的五倍。換句話說,如果你第一題答對,你就獲得5分,而當你第二題回答正確,你測驗的得分只增加了1分,因此從考生的角度而言,第一題會比第二題更為”重要”,因為考生有機會在第一題獲得5分。從命題者的角度來說,第一題也應該是”重要”的題目,因為它能夠區分出學生的能力,這是因為在測驗中得高分應該反映出該學生具有比較高的能力。這種”重要”題目的概念,也應該可以傳達成為”題目的資訊”( item information)。當一道題目有更多的資訊,代表該題能更有效區分高與低能力的學生。換句話說,一道有更多資訊的題目,是一道有更高鑑別度的題目,因為鑑別度就是用來測量題目區分學生能力的程度。
有鑑於此,我們可以嘗試倒過來說,那些有更高鑑別度的題目,他們應該有更高的配分,或者在測驗中有更高的權重。
一般而言,題目鑑別度與題目難度是兩不相干的概念,也就是說,一道題目最高的配分不應該依賴於該題的難度,而是依賴於該題的鑑別度。
一道有很高鑑別度的題目,應屬於”重要”的題目,因為該題與測驗背後所要測量的構念有更密切的關係,因此當要思考如何設定某題的最高配分時,我們可以考慮該題對於測量背後的構念有多重要。舉例來說,當我們想要測量作答者得某些疾病如皮膚癌的傾向有多大,我們會詢問關於皮膚的顏色、頭髮的顏色、眼睛的顏色以及家族癌症史等問題,那些與皮膚癌最直接有關的因素應該得到更高的配分,至於那些與皮膚癌比較沒有那麼相關的因素應該獲得低一點的配分。我們並不會以能夠將頭髮的顏色細分成多少個類別,而據此給頭髮顏色更高的配分;反之,我們需要思考的是,用頭髮顏色來預測罹皮膚癌有多有效。
12.3 編碼與評分
當我們討論作答的類別與評分時,我們需要解釋”編碼”與”評分”的差別。我們通常用”編碼”這個詞來代表學生作答反應的不同類別,雖然”編碼”可能是採用0、1、2、3的方式,這些碼是代號,不一定代表真正的得分。事實上,我們最好能夠建立一套配分的系統,以與編碼的系統相對應。舉例來說,我們可能會用0、1、2、3來代表黑色、棕色、綠色與藍色的瞳孔顏色,但這四個碼相對應的分數可能為”0”、“0”、 “1”、 “2”,或是”0”、“1”、 “1”、 “2”,又或者是其他分數的組合,如何配分應視乎瞳孔顏色與皮膚癌的關係有多密切而定。無論如何,當我們收集資料時,我們可以採用很多”代碼”來反映學生的作答類別,然後按照我們研究的內容與所收集到的資料來判斷如何評分。也就是說,我們不需要設定一個一成不變的配分方式,除非先前的研究已經能夠提供資訊來建立這個評分準則。因此,當我們完成初步的分析之後,我們很可能需要根據分析的結果來考量是否需要更新配分的方式並重新分析。
12.4 部分計分模型(PCM)與雙參數模型(2PL)
事實上,雙參數模型(2PL) 的目的正是要估計各題的題目權重。一些雙參數模型會為每個題目估計題目權重,另外一些雙參數模型則是要估計各個作答類別的權重。在雙參數模型中,“編碼”與”評分”是完全分開的;相較之下,部分計分模型會在事前進行配分,這些配分並非透過估算出來的。再者,這兩個模型另外一個差異在於部分計分模型的評分通常是整數,而雙參數模型對題目類別的評分則可以是任何實數。
12.5 部分計分模型與雙參數模型的例子
在 PISA 2018的資料集中,學生背景問卷中有一個題組,編號為ST197,詢問學生一些題目,是關於他們對全球議題的瞭解程度。更詳細的說,它詢問學生關於以下各方面的小題:
- 氣候變遷與全球暖化(ST197Q01HA)
- 全球範圍的健康問題 (例如流行病) (ST197Q02HA)
- 遷徙 (人口的移動) (ST197Q04HA)
- 國際衝突 (ST197Q07HA)
- 世界不同區域飢餓或營養不良的問題 (ST197Q08HA)
- 造成貧困的原因 (ST197Q09HA)
- 全球不同地區男女平等的問題 (ST197Q12HA)
至於每道題目的作答選項,學生只能四選一:
- 我從來沒有聽說過此議題
- 我有聽說過這個議題,不過我無法解釋它到底是怎麼一回事
- 我對此議題有所了解,可以做大致上的解釋
- 我很熟悉此議題,並且可以解釋得很好
我們隨機挑選了5000位學生對此題組的作答反應,以下分析的過程中,我們並不會採用學生的抽樣權重,因為我們只是想用這個資料集作為分析多元計分題目的例子,我們不打算估計學生的熟練程度(proficiency levels)。該資料集可在此下載,我們將四個選項編碼成 0、1、2、3,這個資料集沒有遺漏值。以下的 R 程式碼採用部分計分模型來對資料進行分析,這七個問題背後的潛在構念是學生留意全球化議題的程度。
rm(list=ls())
library(TAM)
library(WrightMap)
library(knitr)
gble <- read.csv("C:\\G_MWU\\ARC\\Philippines\\files\\globalawareness.csv")
mod1 <- tam.jml(gble)
thres <- tam.threshold(mod1)題目閾值參數 (thres) 為:
| Cat1 | Cat2 | Cat3 | |
|---|---|---|---|
| ST197Q01HA | -3.460602 | -1.6015320 | 1.2336731 |
| ST197Q02HA | -3.723358 | -1.0364685 | 2.0592957 |
| ST197Q04HA | -3.887970 | -1.6253357 | 1.3512268 |
| ST197Q07HA | -3.582367 | -0.9559021 | 1.7822571 |
| ST197Q08HA | -3.860138 | -1.6176453 | 1.3587341 |
| ST197Q09HA | -4.121246 | -1.7271423 | 1.0903015 |
| ST197Q12HA | -3.755035 | -1.8368225 | 0.6665955 |
The Wright Map is shown below:
其能力與難度對應圖(Wright Map)如下所示:
w <- wrightMap(mod1$WLE, thres, item.side = itemClassic)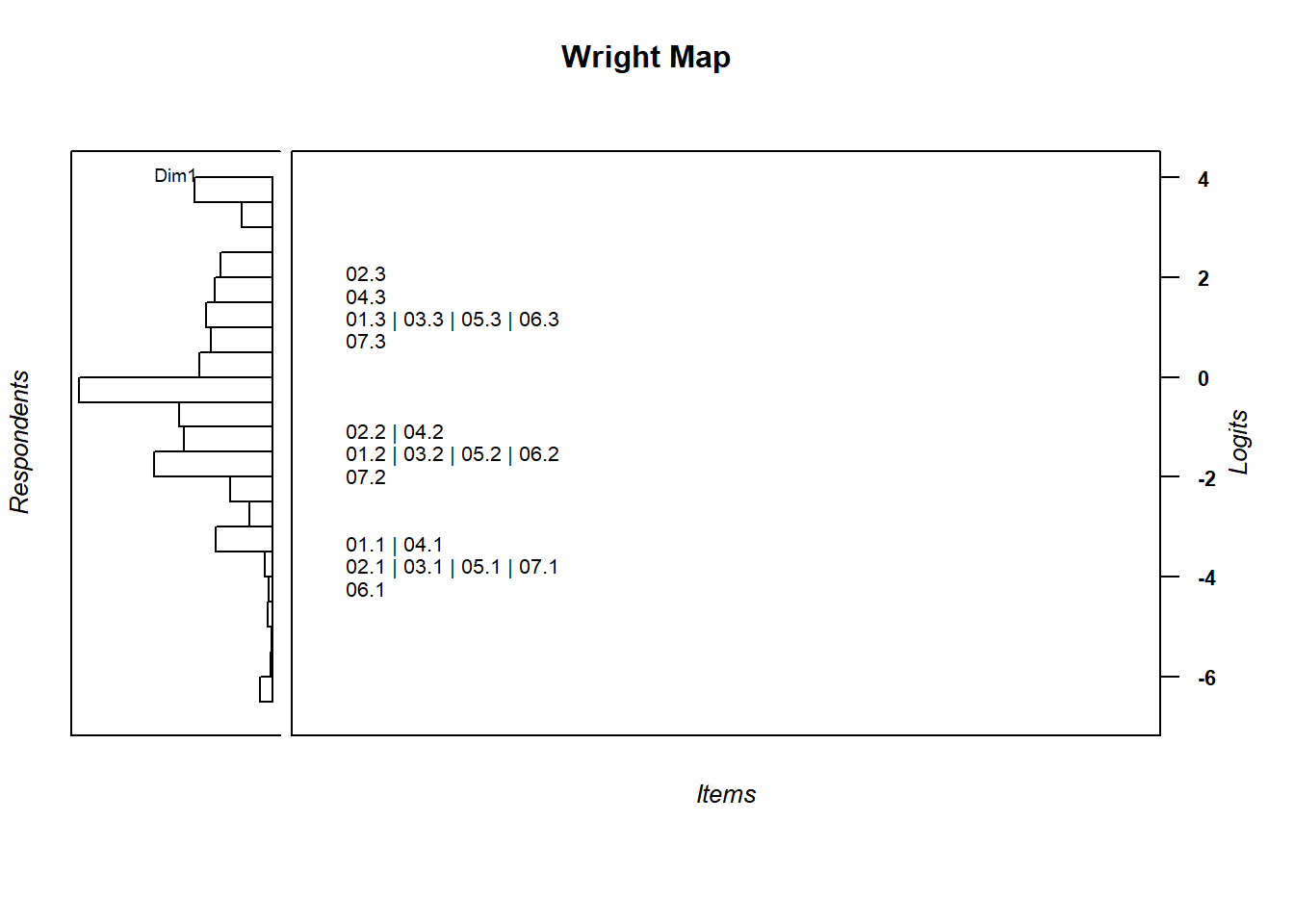
图 12.1: 能力與難度對應圖 Wright Map
這組題目的題目閾值排列很特別,我們可以觀察到各小題得1分的估計值都自成一群,各小題得2分的估計值也自成一群,各小題得3分的估計值也自成一群,這反映出這七個小題的題目難度層級都非常接近。這是否代表我們先前配分的方式是正確的?要回答這個問題,讓我們先計算各小題的題目鑑別度。
score <- apply(gble,1,sum)
disc <- apply(gble,2,function(x){cor(x,score-x)})
discST197Q01HA ST197Q02HA ST197Q04HA ST197Q07HA ST197Q08HA ST197Q09HA ST197Q12HA
0.6178032 0.6491644 0.7038320 0.6351406 0.7207811 0.6963074 0.6324818 各小題的題目鑑別度都非常高,雖然有些題目的鑑別度相對會更高一點。由於各小題都曾經過一個預試,因此各題效果不錯,我們並不訝異。
接下來我們將採用雙參數模型來進行校準,並估計各題得分等級的參數值,以下的 R 指令可以用來進行雙參數模型的估計:
mod2 <- tam.mml.2pl(gble)kable(mod2$B,caption="\u96d9\u53c3\u6578\u6a21\u578b\u4f30\u8a08\u984c\u76ee\u985e\u5225\u7684\u5206\u6578\u0028\u6216\u659c\u7387\u0029\u53c3\u6578 ")| Cat0.Dim01 | Cat1.Dim01 | Cat2.Dim01 | Cat3.Dim01 | |
|---|---|---|---|---|
| ST197Q01HA | 0 | 1.096437 | 2.414818 | 4.013876 |
| ST197Q02HA | 0 | 1.186946 | 2.653121 | 4.887355 |
| ST197Q04HA | 0 | 1.834553 | 3.950712 | 6.581108 |
| ST197Q07HA | 0 | 1.255264 | 2.716831 | 4.765690 |
| ST197Q08HA | 0 | 2.008038 | 4.507274 | 7.653130 |
| ST197Q09HA | 0 | 1.921985 | 4.231949 | 6.895981 |
| ST197Q12HA | 0 | 1.211725 | 2.972841 | 4.668335 |
表12.2呈現第五小題(ST197Q08HA)得分類別的估計值,該等估計值差不多是第一題估計值的一倍,由此可以看出,如果我們採用雙參數模型,則各題的題目類別得分就不太一致了。換句話說,各小題的權重並不相同,雖然它們的題目難度很接近。模型1(mod1$WLEreliability)的題本信度為0.86,而模型2(mod2$EAP.rel)的題本信度為0.88。
12.6 適合度統計量
關於題目類別的估計值,我們也可以透過基於殘差的適合度統計量來做進一步的了解,因為這些適合度統計量與題目的鑑別度有關。1
mod3 <- tam.jml(gble,bias=FALSE)
f1 <- tam.fit(mod3)| ST197Q01 | ST197Q02 | ST197Q04 | ST197Q07 | ST197Q08 | ST197Q09 | ST197Q12 |
|---|---|---|---|---|---|---|
| 1.101 | 1.001 | 0.866 | 1.05 | 0.823 | 0.879 | 1.036 |
上表報導七個小題的Infit均方值,從中可以觀察到第3、5、6題的適合度均方值比較低(overfit),這代表這三道題目的權重可以增加,這個結果與雙參數模型所估計出來的斜率參數值相當一致。
小結:多元計分模型中的題目類別得分是與題目鑑別度有關,而與題目難度沒有關係。
請注意,用來計算適合度的 R 程式碼中,IRT的量尺函數(tam.jml)有一個 bias=FALSE 的選項。一般而言,在估計題目參數的時候,偏誤是應該要接受修正的,因此該函數預設是要執行偏誤修正(bias correction)。然而,該偏誤修正常會導致適合度均方值變得比較小,因此所有估計出來的值都會有低於1的傾向,而非它們的數據會環繞著1,因此我們在這裡將偏誤修正的選項設為否,意思是不執行偏誤修正。↩︎