第 10 章基於殘差的題目適合度統計方法

本節中我們將可以學到:

基於殘差的題目適合度統計方法(Residual-based Item Fit Statistics)
如何在 R 環境中模擬題目反應

我們要到現在才開始討論關於題目適合度的主題，這是有理由的。雖然資料分析其中一個步驟，就是必須確認題目反應的資料是否符合我們所選用的IRT模型，但由於基於殘差的題目適合度統計分析的結果常被誤解，導致具品質的題目被捨棄，這是非常可惜的。我們寧可不進行適合度統計分析，也不要因為誤用該等方法而對題目做出錯誤的結論。反之，如果我們想要使用基於殘差的適合度統計方法，則清楚瞭解這些統計方法的性質是非常重要的。

10.1 基於殘差的題目適合度統計方法

設 \(X_{ni}\) 為第 \(n\) 人對第 \(i\) 題所作的反應。 \(X_{ni}\) 是一個二項式隨機變量(binomial random variable)，取值為 0 和 1。根據Rasch 模型，\(X_{ni}\) 的期望值為 \(E_{ni}=p\) (參 Eq.(3.1)，\(X_{ni}\) 的變異數則為 \(W_{ni}=p(1-p)\)。

對於每一個人 \(n\) 和每一道題目 \(i\) ，Wright 和 Masters (1982) 兩位學者定義了一個　標準化殘差　的統計量，公式如下所示：

\[\begin{equation} z_{ni} = \frac{x_{ni}-E_{ni}}{\sqrt{W_{ni}}}\tag{10.1} \end{equation}\]

\(z_{ni}\) 看起來很像是一個 \(z\)-分數，只不過 \(x_{ni}\) 是一個離散量的變數（其值只為 0 或 1），而不是一個連續量的變數。然而，\(z_{ni}\) 具有的分佈性質類似於\(z\)-分數的分佈性質。

Wright 和 Masters (1982) 兩位學者進一步定義了一個基於殘差的題目適合度統計量，公式如下所示：

\[\begin{equation} u_i = \frac{ \sum\limits_{n=1}^{N} z_{ni}^2 }{N}\tag{10.2} \end{equation}\]

其中 \(N\) 是學生總人數。我們稱\(u_i\)為 未加權適合度均方(unweighted fit mean square) 或 outfit。“outfit” 一詞是提醒大家注意此統計量對極端值(outlier)尤其敏感。如果某人對某題目的反應是超乎預期的，例如一個能力很強的學生在一道簡單題目上寫出錯誤的答案，又或者是一個能力很弱的學生正確地回答了一道困難的題目，則他們所對應的適合度均方(fit mean square) 的值很可能會很大。由此可見，一道題目有可能是由於有一些偶然出現的極端值的緣故而被認為不合適。為了解決此一敏感於極端值的問題，Wright 和 Masters另外定義了 加權適合度均方(weighted fit mean square)　，公式如下所示：

\[\begin{equation} v_i = \frac{ \sum\limits_{n=1}^{N} W_{ni}z_{ni}^2 }{\sum\limits_{n=1}^{N} W_{ni}}\tag{10.3} \end{equation}\]

Eq.(10.3) 中的權重 \(W_{ni}\) 是 \(X_{ni}\) 的變異數。當學生的能力值與題目的難度相匹配時，\(W_{ni}\) 的值會比較大，但當學生的能力值和題目難度相距甚遠時， \(W_{ni}\) 的值會比較小。 \(v_i\) 可稱為 加權適合度均方（weighted fit mean square），或稱為 infit 以代表“信息加權適合度(information weighted fit)” 的意思，原因是 \(W_{ni}\) 亦稱為信息函數(information function)。

10.2 適合度均方（fit MS）統計量的臨界值

為了能夠應用適合度統計量來評估題目反應資料是否符合某一模型，我們需要知道當題目反應資料確實符合該模型時，其適合度統計量會落在什麼範圍。我們可以從統計理論或電腦模擬中估計出這些臨界值，以下我們將進行一些電腦模擬，藉以找出當題目反應符合 Rasch 模型時，其適合度統計量的分佈特性為何。我們將產生符合 Rasch 模型的題目反應資料，首先產生2000名學生的題目反應數據，他們的能力值是從 N(0,1) 的標準常態分佈中隨機抽取而得，另外，我們模擬 40 道題目，它們的難度值是從 -2 到 2以等差數列的方式遞增。接著，我們計算每道題目的outfit值，然後重複100次電腦模擬。因此對於每道題，我們總共會產生100 個outfit均方值，並計算每一道題目outfit值的平均值，以及每一道題目100個outfit值的標準差。

library(TAM)
generateRasch <- function(N,I){
  theta <- rnorm( N ) # student abilities
  p1 <- plogis( outer( theta , seq( -2 , 2 , len=I ) , "-" ) )  #從 -2 到 2的題目難度遞增值
  resp <- 1 * ( p1 > matrix( runif( N*I ) , nrow=N , ncol=I ) )  #題目反應
  colnames(resp) <- paste("I" , 1:I, sep="")
  return(list(resp=resp))
}

simulateFit <- function(N,I,Nrep){
  outfit <- matrix(0,ncol=I,nrow=Nrep)
  colnames(outfit) <- paste0("Item",seq(1,I))
  for (r in 1:Nrep){
    d <- generateRasch(N,I)
    mod1 <- tam.jml(d$resp,bias=FALSE)
    fit1 <- tam.jml.fit(mod1,trim_val = NULL)
    outfit[r,] <- fit1$fit.item$outfitItem
  }
  return (list(outfitMS=outfit))
}
set.seed(26473)
N <- 2000
I <- 40
Nrep <- 100
s <- simulateFit(N,I,Nrep)
apply(s$outfitMS,2,mean)
apply(s$outfitMS,2,sd)

上述模擬結果表明，outfit均方統計量的平均值非常接近1，而標準差的範圍是從 0.0251 到 0.0744，而這些標準差的平均值為 0.0426。由此可見，當樣本數為2000時，如果題目反應資料符合 Rasch 模型時，95% 的outfit均方值很可能會介於 0.92 和1.08 之間。

以下呈現我們100次模擬中的其中一次(即第二個replication) ，40 道題目outfit值分散程度的點狀圖形(Figure 10.1)。

dotchart(s$outfitMS[2,], xlim=c(0.5,1.5), pt.cex=1, cex=0.5)
abline(v=0.9,lty=3)
abline(v=1.1,lty=3)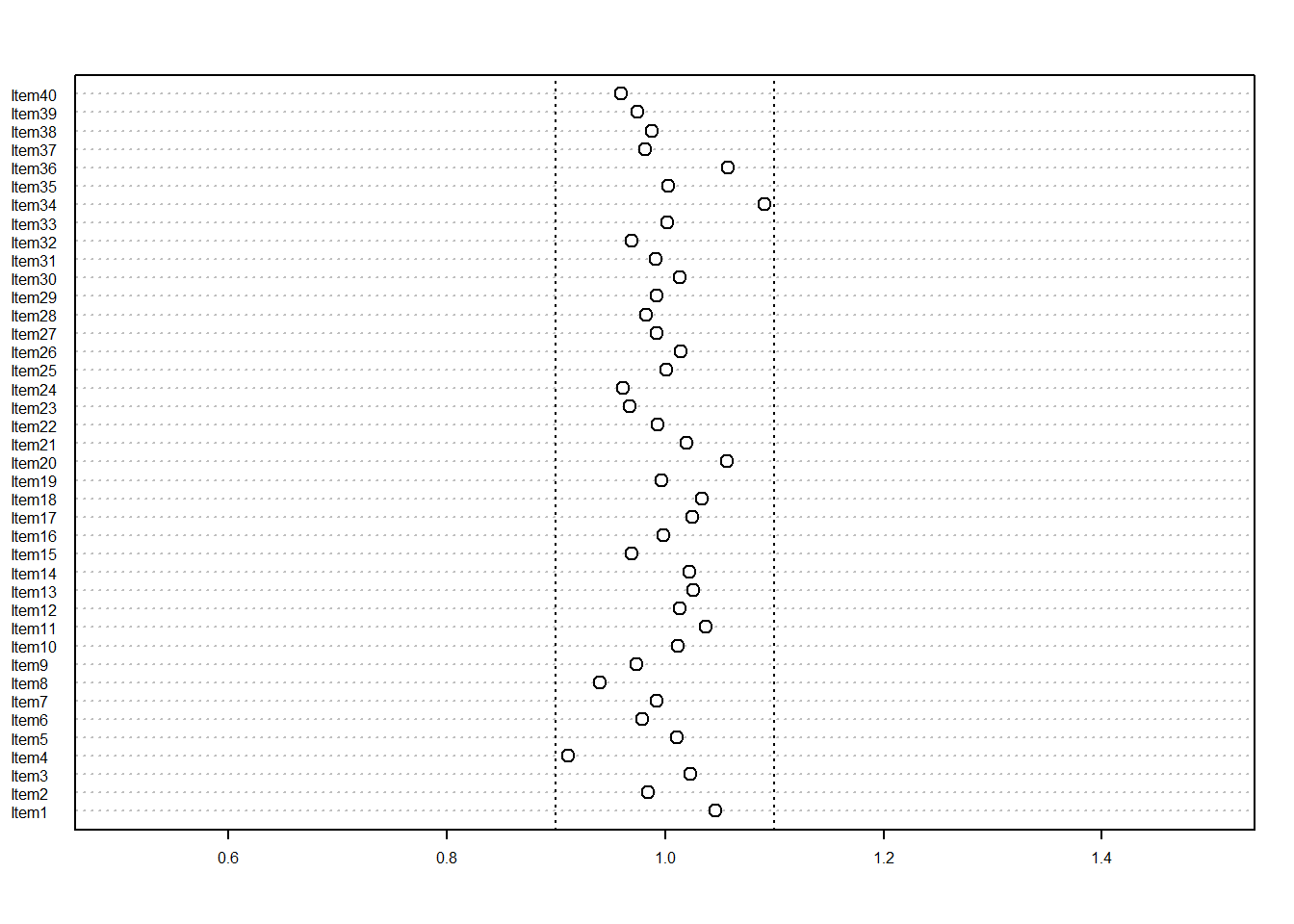

图 10.1: 當樣本數為2000人時的outfit均方值

然而，當我們用 500 名學生作為樣本數來重複整個電腦模擬後，會發現outfit均方值的分佈範圍顯得比較寬廣，如圖 10.2 所示。

set.seed(4625)
N <- 500
I <- 40
Nrep <- 100
s <- simulateFit(N,I,Nrep)

dotchart(s$outfitMS[2,], xlim=c(0.5,1.5), pt.cex=1, cex=0.5)
abline(v=0.8,lty=3)
abline(v=1.2,lty=3)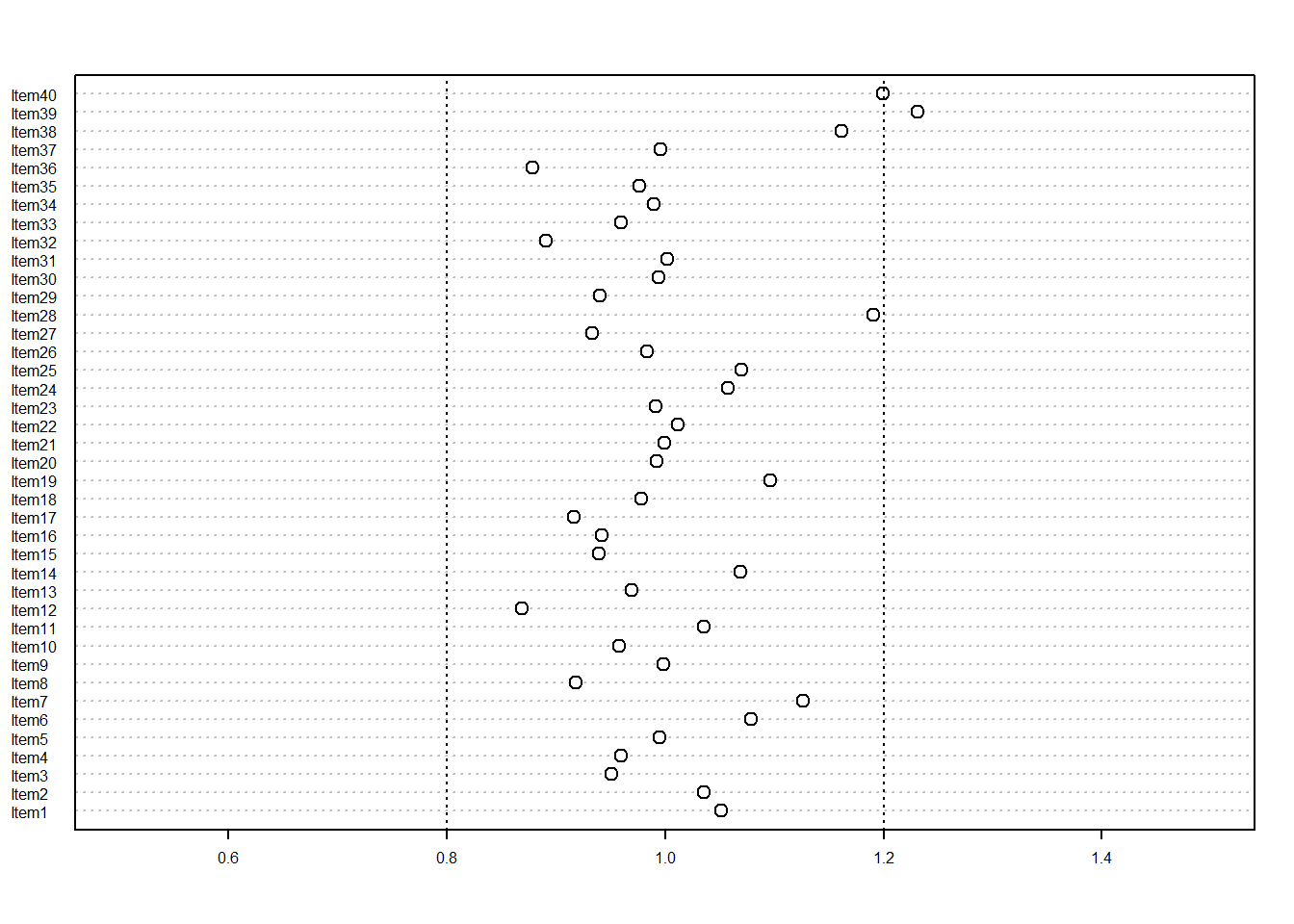

图 10.2: 當樣本數為500人時的outfit均方值

比較這兩個圖形，我們會發現，判斷題目是否符合 Rasch 模型的臨界值是有賴於學生的樣本數。樣本數較小時，適合度均方值的範圍較大。反之，當樣本數較大（比如超過5000個學生）時，適合度均方值就會非常接近 1。因此，我們很難建立一套絕對的臨界值參考準則，藉以判斷不適合的題目，這是因為我們還需要將樣本數的大小考慮在內。實務上，我們可以用以下簡單的公式，來近似地估計臨界值。

\[\begin{equation} Asymptotic\: standard\: error\: for\: outfit\: MS = \sqrt {\frac{2}{N}}\tag{10.4} \end{equation}\]

其中 \(N\) 是學生的樣本數。例如，當樣本數為 2000 時，其漸近標準誤(asymptotic standard error)為0.032，因此接受題目為適合Rasch模型的範圍是設在 0.94 到 1.06之間。相較之下，當樣本數為 500 時，漸近標準誤為 0.063，因此接受題目為適合Rasch模型的範圍是設在 0.87 到 1.13之間。

TAM 套件處理極端值的補充說明 在 TAM 套件中，用來計算基於殘差的適合度統計量的函數，它具有一個引數(argument) 項可以用截尾的方式刪除極端值。一般情況下，引數 trim_val 的預設值為 10，只要標準化殘差值的平方值大於 trim_val 時，其值就會被設置為 trim_val。我們建議採用此選項，這樣就不會因為偶然出現的極端值而導致適合度均方值過高。但是為了方便這裡的說明，上述用於檢查適合度均方值分佈屬性的 R 編碼中，我們已關閉此選項。

10.3 該採用Infit 還是 Outfit?

不同的研究者對於應該採用Infit 還是 Outfit有不同的建議。前面我們有提到outfit有可能受偶然出現的極端值影響，導致出現過高的適合度均方值，我們的建議是infit比outfit更為可取，以免我們因為受隨機性的影響而不小心將適合的題目誤判成不適合，儘管這樣做可能會讓我們在判斷上變得比較保守。

10.4 題目不適配的兩種情況：underfit 和 overfit

當題目符合 Rasch 模型時，它們的適合度均方值會接近1，因此不符合 Rasch 模型的題目，其適合度均方值可能會遠小於1，或者遠大於1。對於那些適合度均方值遠大於1的題目，它們被稱為是 低適配（underfit) 的。至於那些適合度均方值遠小於 1 的題目，它們被稱為是 過度適配(overfit) 的。在我們討論低適配和過度適配前，我們將首先解釋適合度均方統計量可以檢測出什麼資訊與無法檢測出什麼資訊。

對於透過適合度均方值判斷為不適合Rasch模型的題目，常有人誤會它是指理論上的題目特徵曲線(ICC)與實務上觀察到的題目特徵曲線兩者之間沒有互相重疊。我們以下圖10.3 為例呈現在 CTTdata 中第四題的題目特徵曲線。

library(TAM)
library(CTT)
data(CTTdata)
data(CTTkey)
CTTresp <- score(CTTdata, CTTkey, output.scored = TRUE)
IA <- itemAnalysis(CTTresp$scored)

mod2 <- tam.jml(CTTresp$scored)
fit2 <- tam.jml.fit(mod2)

plot(mod2,items=4)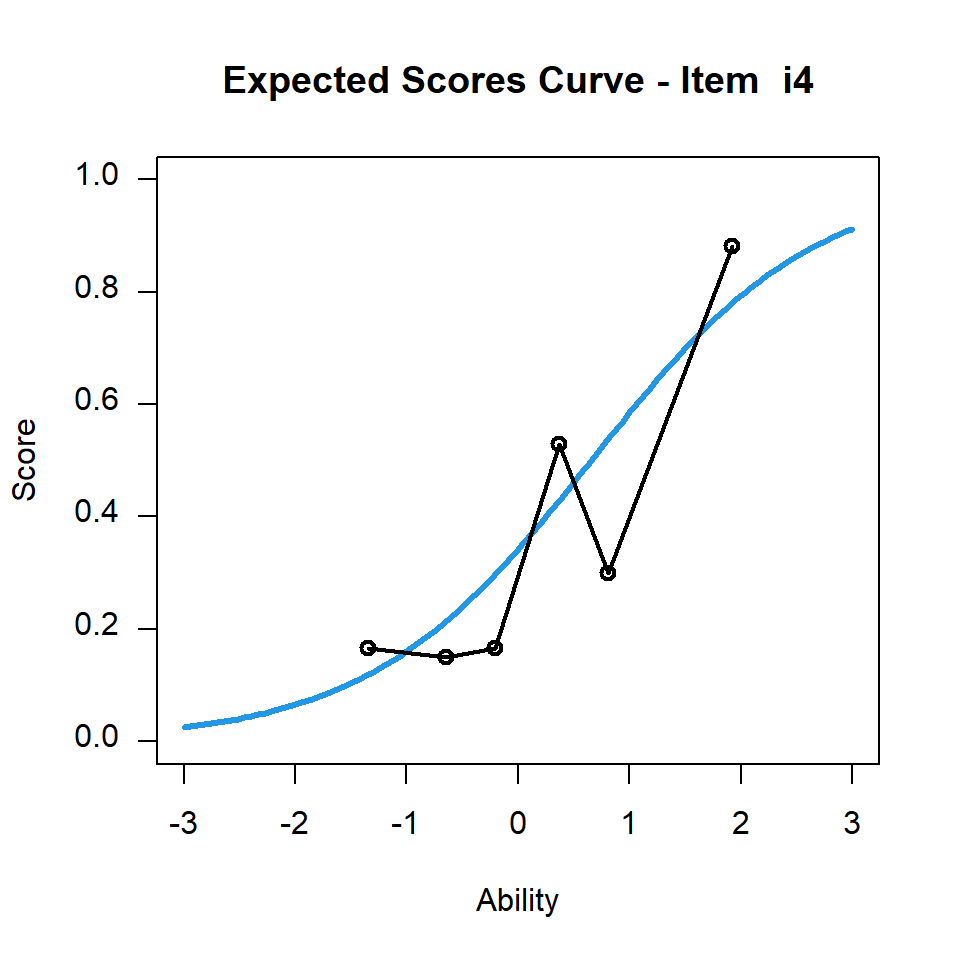

图 10.3: CTTdata中第四題的題目特徵曲線

在圖10.3中，理論上的題目特徵曲線和觀察到的題目特徵曲線似乎並沒有互相重疊，可是其infit均方值為 0.924。為了方便比較，我們另外透過圖10.4來呈現同一題的題目特徵曲線，但是為了要與圖10.3做比較，我們將六個學生能力族群改成四個學生能力族群，藉以呈現該題觀察到的題目特徵曲線。

plot(mod2,items=4,ngroups=4)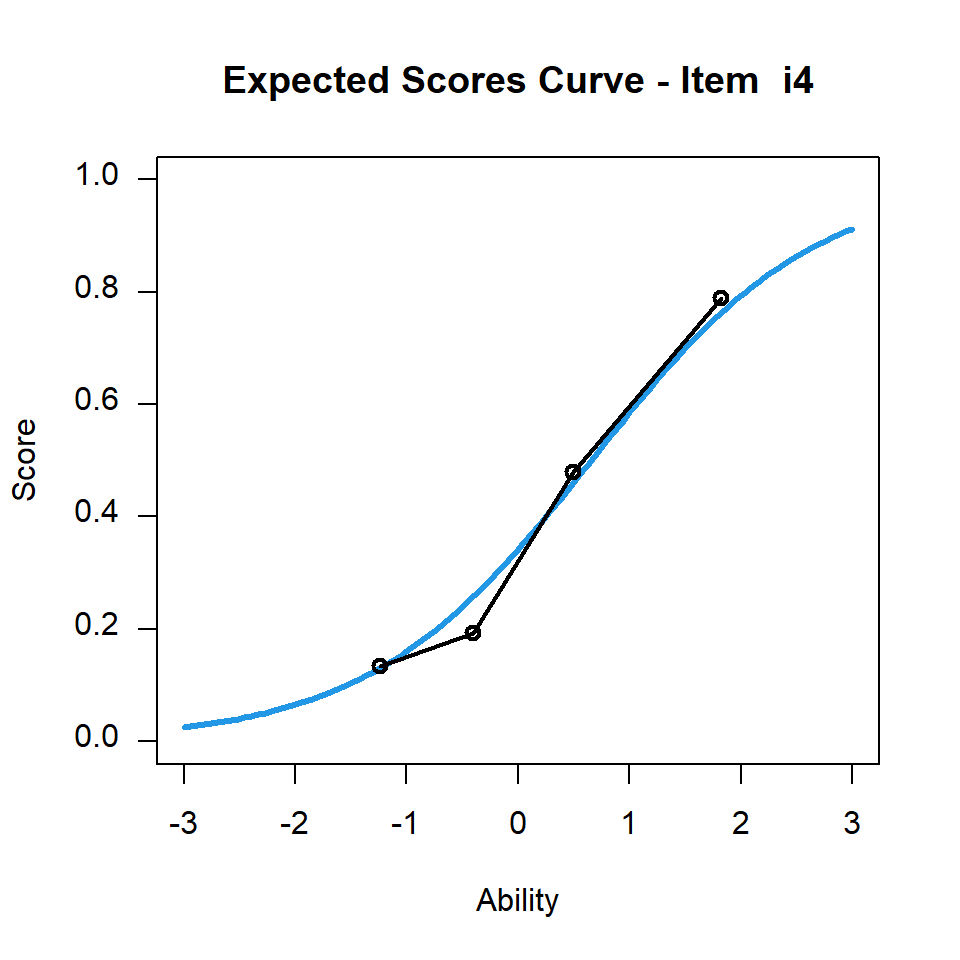

图 10.4: CTTdata第四題的題目特徵曲線

圖 10.4呈現觀察到的與理論上的題目特徵曲線非常接近，由於 CTTdata 的資料集總共只有100名學生，因此若將學生分成更多組別，即代表每一組內的學生人數會很少，每組別人數的多寡，導致組別間平均得分會有比較大的波動。針對這個例子，當我們將學生只分成四組時，每一組別的學生數就會更多，而四組學生可觀察到的平均得分與理論上的平均得分更為接近。由此可見，判斷理論上與觀察到的題目特徵曲線是否適合，用肉眼檢查並不是一個適當的方法。一般而言，我們建議在繪製觀察到的題目特徵曲線圖時，採用組別比較少來繪製會優於用組別比較多的。

對於 CTTdata，我們將適合度統計量報導於表10.1中。

library(knitr)
kable(fit2$fit.item,digits=3,align="ccccc",
      caption="\u0043\u0054\u0054\u0064\u0061\u0074\u0061\u7684\u984c\u76ee\u9069\u5408\u5ea6\u7d71\u8a08\u8868 ",row.names=FALSE)

表 10.1: CTTdata的題目適合度統計表
item	outfitItem	outfitItem_t	infitItem	infitItem_t
i1	0.741	-1.621	0.835	-1.831
i2	0.823	-0.975	0.887	-1.280
i3	1.114	0.642	1.173	1.876
i4	1.037	0.264	0.924	-0.671
i5	0.958	-0.180	1.029	0.297
i6	0.754	-0.507	0.977	-0.105
i7	0.651	-1.312	0.816	-1.895
i8	0.937	-0.261	1.007	0.114
i9	1.100	0.535	1.098	0.808
i10	1.031	0.233	1.123	1.343
i11	0.798	-1.206	0.869	-1.295
i12	0.836	-0.796	0.801	-2.398
i13	1.142	0.686	1.068	0.778
i14	0.773	-1.316	0.844	-1.801
i15	1.235	1.305	1.152	1.392
i16	1.438	2.024	1.316	2.451
i17	0.883	-0.657	0.920	-0.771
i18	0.960	-0.137	0.984	-0.092
i19	1.207	1.074	1.052	0.474
i20	1.082	0.522	0.968	-0.281

適合度均方檢測的目的，是要檢測觀察到的題目特徵曲線是否比理論上的題目特徵曲線來得陡，還是比較平坦。若要進一步了解，可參考(Wu and Adams 2013) 的著作。以下的討論，我們將檢查infit 值而非outfit值。請留意表10.1中的第16題，其infit 均方值大於1，圖10.5則呈現該題的題目特徵曲線。

plot(mod2,items=16,ngroups=3)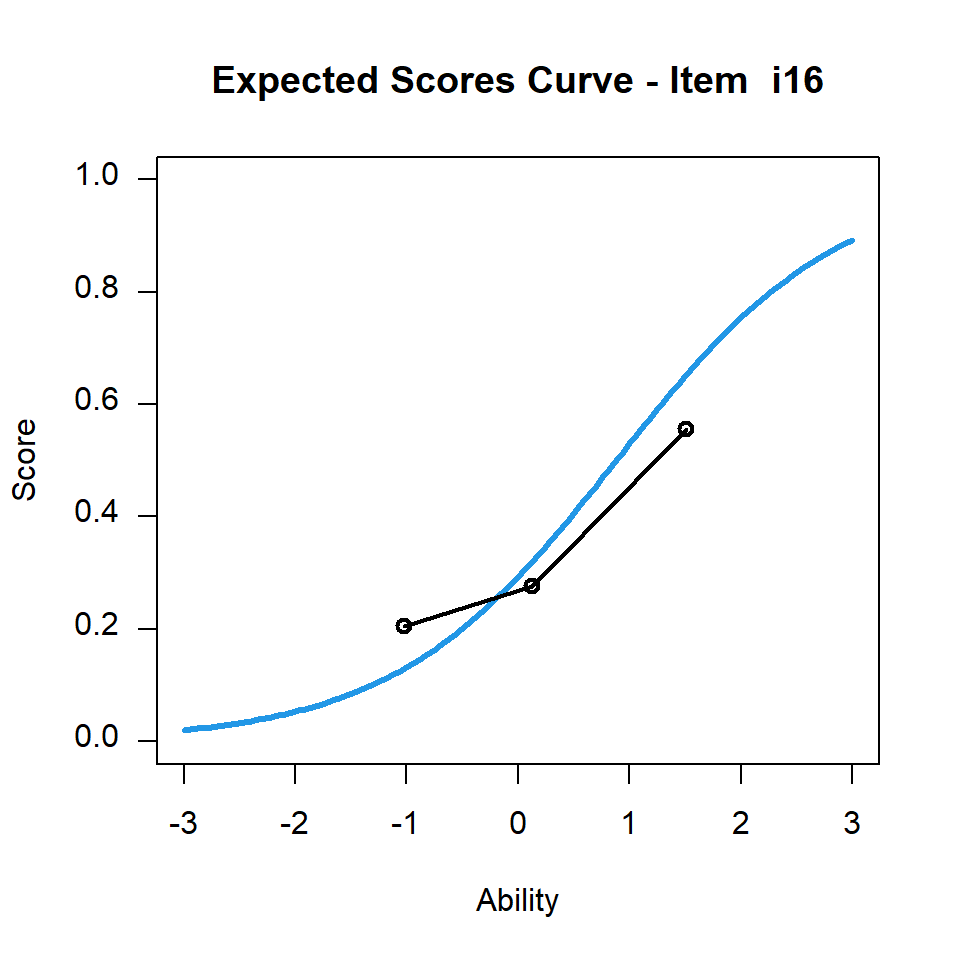

图 10.5: CTTdata第16題的題目特徵曲線

相較之下，第12題的infit均方值小於1，圖10.6則呈現該題的題目特徵曲線。

plot(mod2,items=12,ngroups=3)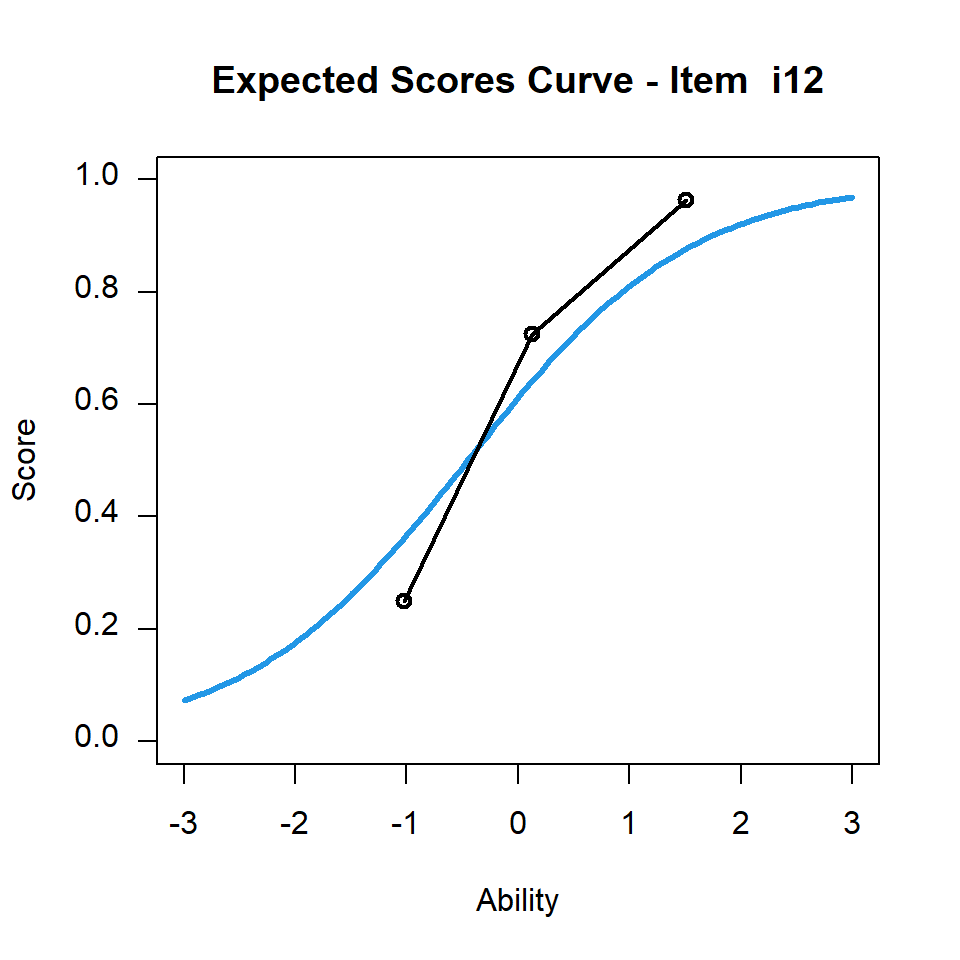

图 10.6: CTTdata第12題的題目特徵曲線

10.5 基於殘差的適合度統計量可反映題目的鑑別度

基於殘差的適合度統計量基本上是反映題目特徵曲線的斜率:

當適合度均方值接近1，代表該題的鑑別度會等於該組題目的平均鑑別度.
當適合度均方值小於1，代表該題的鑑別度大於該組題目的平均鑑別度.
當適合度均方值大於1，代表該題的鑑別度小於該組題目的平均鑑別度.

有鑑於此，高品質的題目是指其適合度均方值小於1的題目，即使它們當中有些題目的鑑別度高於平均而被視為是 不適配於 Rasch模型。至於那些適合度均方值大於1的題目，其實是比較弱的題目，因為與其它題目相比，它們比較不能有效地鑑別出學生能力。最後，那些被認為是適合 Rasch模型 (適合度均方值接近1) 的題目，其實是普通的題目，因為它們的鑑別度只等於平均的鑑別度。

在實務上，一個常見的錯誤是很多研究者會將適合度均方值大於或小於1的題目刪除，只保留適合度均方值接近1的題目．這樣處理的方式很可能會刪除一些品質非常好的題目，這是很可惜的。

10.6 適合度均方值是相對的

適合度均方值是相對性的統計量，其值是相對於題組中所有題目適合度的值而言。如果我們抽取一部分的題目重新分析，這組題目當中適合度均方值接近1的題目，很可能和原先接近1的題目不同。舉例來說，以下我們只選擇適合度均方值小於1的題目，並重跑一次分析。

resp3 <- CTTresp$scored[,fit2$fit.item[,4]<1]
colnames(resp3) <- paste("Item ",which(fit2$fit.item[,4]<1))
mod3 <- tam.jml(resp3)
fit3 <- tam.jml.fit(mod3)

kable(fit3$fit.item,digits=3,align="ccccc",
      caption="\u0043\u0054\u0054\u0064\u0061\u0074\u0061\u4e2d\u984c\u76ee\u9069\u5408\u5ea6\u5747\u65b9\u503c\u5c0f\u65bc\u0031\u7684\u984c\u76ee ",
      row.names=FALSE)

表 10.2: CTTdata中題目適合度均方值小於1的題目
item	outfitItem	outfitItem_t	infitItem	infitItem_t
Item 1	0.888	-0.407	0.903	-0.812
Item 2	1.001	0.091	0.974	-0.202
Item 4	1.040	0.241	1.001	0.054
Item 6	0.702	-0.386	0.988	-0.040
Item 7	0.679	-0.786	0.885	-1.066
Item 11	0.962	-0.080	1.004	0.074
Item 12	0.718	-1.018	0.826	-1.694
Item 14	0.827	-0.646	0.918	-0.716
Item 17	0.822	-0.708	0.974	-0.166
Item 18	1.096	0.427	1.171	1.221
Item 20	1.108	0.512	1.044	0.386

表10.2所報導的infit均方值，是針對表10.1中infit均方值小於1的題目，但當我們僅重新估計該組題目的infit均方值，卻可以觀察到所有題目的infit均方值皆已經比較接近1。

在表10.1中，如果我們只選擇infit均方值大於1的題目，並重新進行分析，我們可以在表10.3中觀察到，所有題目的infit均方值已經圍繞著1。

resp4 <- CTTresp$scored[,fit2$fit.item[,4]>1]
colnames(resp4) <- paste("Item ",which(fit2$fit.item[,4]>1))
mod4 <- tam.jml(resp4)
fit4 <- tam.jml.fit(mod4)

kable(fit4$fit.item,digits=3,align="ccccc",
      caption="\u5c0d\u0043\u0054\u0054\u0064\u0061\u0074\u0061\u4e2d\u9069\u5408\u5ea6\u5747\u65b9\u503c\u5927\u65bc\u0031\u7684\u984c\u76ee\uff0c\u91cd\u65b0\u9032\u884c\u6821\u6e96\u5f8c\u7684\u9069\u5408\u5ea6\u5747\u65b9\u503c",
      row.names=FALSE)

表 10.3: 對CTTdata中適合度均方值大於1的題目，重新進行校準後的適合度均方值
item	outfitItem	outfitItem_t	infitItem	infitItem_t
Item 3	1.041	0.303	1.086	1.109
Item 5	0.797	-1.323	0.889	-1.209
Item 8	0.909	-0.511	0.961	-0.489
Item 9	0.811	-1.038	0.881	-1.084
Item 10	0.900	-0.619	0.964	-0.448
Item 13	0.960	-0.160	1.014	0.202
Item 15	1.126	0.827	1.088	0.968
Item 16	1.058	0.386	1.107	1.019
Item 19	0.840	-0.933	0.859	-1.409

在前述兩個表格中，雖然所有適合度均方值都環繞著1，但無論我們是重新校準所有適合度均方值大於1的題目或是小於1的題目，它們之間卻有很大的差異，事實上它們的信度差異很大。對於適合度均方值小於1的這組題目，其重新校準後的信度係數為0.691。相較之下，對於適合度均方值大於1的題目，經重新校準後的信度係數則為 0.347 ；而在表10.1 中，所有題目的信度係數為0.779 。這是一個重要原因，我們希望能夠藉此說明為什麼不宜刪除適合度均方值小於1的題目。

10.7 適合度 t 考驗

在表10.1 、 10.2 、 10.3中，都有輸出兩欄名為”outfitItem_t” 和 “infitItem_t”的數據，它們是適合度 t 考驗的數據，它們是經由將適合度均方值轉換成為z分數。換句話說，適合度 t 考驗可以視為是一個N(0,1) 的變數。如果該數值落在(-2, 2)之外，則我們可以說該適合度均方值在統計上達顯著水準，其值顯著有別於1。將適合度均方值轉換到z分數的過程中，就已經有考量到學生的樣本數\(N\)。所以無論樣本數為何，適合度t考驗可以視為是一個服從N(0,1) 的變數。這樣的詮釋頗為有用，因為適合度均方統計量的臨界值是取決於樣本數。但對於適合度t考驗而言，我們大致上可以檢查它的值是否落在(-2, 2)這個區間內，這是一個很方便的處理方式，因為我們並不需要擔心因樣本數不同而會有不同臨界值的困擾。然而，在實務上，還是有其它問題需要考量，這反映出理論與實務上處理問題時，常會出現一些差異，我們在以下的章節做進一步的說明。

10.8 真實數據與模擬數據的比較

當我們根據Rasch模型來產生一些模擬數據時，我們可以用前述介紹的理論分佈性質與假設考驗來分析該等資料。但在現實生活中，我們收集到的題目反應資料通常並不符合Rasch模型的要求(即所有題目的鑑別度要相同)。根據我們的經驗，我們還沒有碰過一組真實的資料會完全符合Rasch模型，不同的題目通常鑑別能力並不相同。這情況與題目的難度不太一樣，通常命題者比較能夠控制所命題目的難度，然而，很少有命題者能夠預測他所命題目的鑑別度為何，更不要說要命出一道具有特定鑑別度的題目。因此在實務上，當我們要運用Rasch模型時，我們就要容忍題目鑑別度可能有所不同，但從統計的角度而言，如果我們所收集資料的樣本數夠大，該等題目的適合度t考驗很可能都會達統計上的顯著水準，這只不過是反映「真實」的情況，即題目的鑑別度有所不同，當樣本數足夠大時，幾乎所有的適合度t考驗都達顯著水準。

接著我們提供PISA 2012年數學科的第十個題本作為例子，以做更具體的說明，請在此下載其作答反應。以下的 R 程式碼可以讀取該資料檔，使用tam.jml指令來進行校準，並計算基於殘差的題目適合度統計量。

rm(list=ls())
library(TAM)
setwd("C:\\G_MWU\\ARC\\Philippines\\files")
resp <- read.csv("PISA2012MathBk10.csv")
mod5 <- tam.jml(resp)
fit5 <- tam.jml.fit(mod5)

kable(fit5$fit.item,digits=3,align="ccccc",
      caption="\u0050\u0049\u0053\u0041\u0020\u0032\u0030\u0031\u0032\u5e74\u6578\u5b78\u79d1\u7b2c\u5341\u500b\u984c\u672c\u984c\u76ee\u9069\u5408\u5ea6\u7d71\u8a08\u91cf ",row.names=FALSE)

表 10.4: PISA 2012年數學科第十個題本題目適合度統計量
item	outfitItem	outfitItem_t	infitItem	infitItem_t
PM00KQ02	0.868	-5.001	0.945	-5.328
PM033Q01	1.095	6.724	1.050	7.991
PM034Q01T	0.897	-7.848	0.957	-6.525
PM155Q01	0.861	-14.248	0.887	-21.499
PM155Q02D	1.121	6.836	1.080	10.272
PM155Q03D	0.704	-11.043	0.933	-6.018
PM155Q04T	1.041	3.970	1.030	5.375
PM273Q01T	1.188	17.986	1.136	24.156
PM408Q01T	1.011	0.887	1.037	6.011
PM411Q01	0.788	-20.635	0.873	-22.842
PM411Q02	1.179	15.662	1.095	15.883
PM420Q01T	1.120	11.534	1.082	14.725
PM442Q02	0.721	-21.044	0.841	-24.614
PM446Q01	0.857	-13.480	0.885	-21.567
PM446Q02	0.444	-14.981	0.804	-12.267
PM447Q01	0.936	-5.768	0.977	-4.220
PM462Q01D	0.813	-5.042	0.989	-0.837
PM464Q01T	0.629	-22.206	0.818	-24.482
PM474Q01	1.161	13.325	1.057	9.838
PM559Q01	1.141	11.589	1.102	17.498
PM800Q01	1.424	10.933	1.072	5.626
PM803Q01T	0.630	-22.548	0.822	-23.740
PM828Q01	0.857	-10.531	0.958	-6.519
PM828Q02	1.048	4.612	1.019	3.489
PM828Q03	1.020	1.360	1.076	11.175
PM906Q01	0.994	-0.575	1.008	1.578
PM906Q02	0.862	-7.499	0.951	-6.365
PM915Q01	1.202	15.891	1.050	8.283
PM915Q02	0.916	-6.920	0.920	-14.094
PM982Q01	1.245	8.187	1.012	1.169
PM982Q02	1.125	9.119	1.125	19.168
PM982Q03T	1.194	15.448	1.088	15.089
PM982Q04	0.963	-3.810	0.936	-12.098
PM992Q01	0.922	-4.938	1.002	0.326
PM992Q02	0.853	-7.097	0.916	-10.021
PM992Q03	0.421	-18.975	0.766	-17.681

從表10.4可以觀察到，幾乎所有的infit t統計量都落在(-2, 2)區間外，這是因為該組資料的樣本數(35421)非常大，導致該等適合度t考驗的統計考驗力(power)很強，即使適合度均方值與1的差別非常小，但是仍然可以檢測出來。

接下來，我們再從”PISA2012MathBk10.csv”檔案中隨機抽取1000位學生，再重新進行校準。

sample1000 <- sample(seq(1:nrow(resp)), 1000)
resp1000 <- resp[sample1000, ]
mod6 <- tam.jml(resp1000)
fit6 <- tam.jml.fit(mod6)

kable(fit6$fit.item,digits=3,align="ccccc",
      caption="\u0050\u0049\u0053\u0041\u0020\u0032\u0030\u0031\u0032\u5e74\u6578\u5b78\u79d1\u62bd\u53d6\u0031\u0030\u0030\u0030\u4f4d\u8003\u751f\u7684\u9069\u5408\u5ea6\u7d71\u8a08\u91cf ",
      row.names=FALSE)

表 10.5: PISA 2012年數學科抽取1000位考生的適合度統計量
item	outfitItem	outfitItem_t	infitItem	infitItem_t
PM00KQ02	0.860	-0.847	0.914	-1.404
PM033Q01	0.998	0.005	1.015	0.409
PM034Q01T	0.969	-0.350	1.019	0.494
PM155Q01	0.830	-3.026	0.879	-3.826
PM155Q02D	1.133	1.346	1.111	2.407
PM155Q03D	0.629	-2.208	0.897	-1.492
PM155Q04T	1.067	1.140	1.044	1.345
PM273Q01T	1.201	3.342	1.131	3.934
PM408Q01T	1.069	0.915	1.074	2.014
PM411Q01	0.876	-1.953	0.911	-2.677
PM411Q02	1.222	3.435	1.106	3.087
PM420Q01T	1.123	2.089	1.073	2.235
PM442Q02	0.718	-3.586	0.833	-4.440
PM446Q01	0.884	-1.817	0.921	-2.341
PM446Q02	0.435	-2.484	0.793	-2.159
PM447Q01	0.976	-0.328	1.010	0.289
PM462Q01D	0.695	-1.287	0.914	-1.082
PM464Q01T	0.662	-3.448	0.851	-3.408
PM474Q01	1.189	2.876	1.056	1.638
PM559Q01	1.106	1.597	1.112	3.165
PM800Q01	1.206	0.968	1.082	1.017
PM803Q01T	0.626	-3.445	0.810	-4.049
PM828Q01	0.881	-1.454	0.972	-0.703
PM828Q02	0.983	-0.274	0.953	-1.454
PM828Q03	1.012	0.178	1.133	3.361
PM906Q01	0.960	-0.671	0.978	-0.658
PM906Q02	0.877	-1.084	0.983	-0.356
PM915Q01	1.224	2.979	1.018	0.524
PM915Q02	0.879	-1.714	0.927	-2.067
PM982Q01	1.166	1.036	0.959	-0.659
PM982Q02	1.129	1.655	1.125	3.292
PM982Q03T	1.160	2.264	1.075	2.102
PM982Q04	1.069	1.209	0.990	-0.296
PM992Q01	0.701	-3.180	0.881	-2.782
PM992Q02	0.829	-1.532	0.932	-1.450
PM992Q03	0.413	-3.164	0.758	-3.045

我們可以從表10.5觀察到，它的infit t考驗值皆小於表10.4相對應的值，雖然還是有很多考驗值落在(-2, 2) 的區間外。

再接下來，我們透過表 10.6來報導隨機抽取200位學生，經校準後的題目infit t考驗值。

sample200 <- sample(seq(1:nrow(resp)), 200)
resp200 <- resp[sample200, ]
mod7 <- tam.jml(resp200)
fit7 <- tam.jml.fit(mod7)

kable(fit7$fit.item,digits=3,align="ccccc",
      caption="\u0050\u0049\u0053\u0041\u0020\u0032\u0030\u0031\u0032\u5e74\u6578\u5b78\u79d1\u96a8\u6a5f\u62bd\u53d6\u0032\u0030\u0030\u4f4d\u5b78\u751f\u7684\u9069\u5408\u5ea6\u7d71\u8a08\u91cf",
      row.names=FALSE)

表 10.6: PISA 2012年數學科隨機抽取200位學生的適合度統計量
item	outfitItem	outfitItem_t	infitItem	infitItem_t
PM00KQ02	1.095	0.410	1.053	0.428
PM033Q01	0.848	-0.924	0.971	-0.326
PM034Q01T	0.714	-2.066	0.829	-2.101
PM155Q01	0.753	-2.178	0.842	-2.335
PM155Q02D	0.935	-0.272	1.072	0.779
PM155Q03D	0.751	-0.592	0.886	-0.718
PM155Q04T	1.155	1.371	1.115	1.632
PM273Q01T	1.103	0.961	1.086	1.289
PM408Q01T	1.015	0.148	1.079	0.958
PM411Q01	0.877	-1.118	0.920	-1.170
PM411Q02	0.953	-0.357	0.959	-0.553
PM420Q01T	1.157	1.422	1.133	1.932
PM442Q02	0.770	-1.688	0.887	-1.412
PM446Q01	0.939	-0.341	0.862	-1.751
PM446Q02	0.496	-1.102	0.830	-0.763
PM447Q01	0.963	-0.258	1.006	0.115
PM462Q01D	1.472	1.115	1.082	0.531
PM464Q01T	0.406	-2.734	0.672	-2.883
PM474Q01	1.109	0.925	1.128	1.777
PM559Q01	1.130	0.896	1.115	1.456
PM800Q01	1.258	0.671	1.100	0.554
PM803Q01T	0.688	-1.642	0.888	-1.092
PM828Q01	0.686	-2.132	0.829	-2.100
PM828Q02	1.045	0.444	0.989	-0.142
PM828Q03	0.964	-0.252	0.979	-0.265
PM906Q01	0.894	-0.844	0.994	-0.063
PM906Q02	0.973	-0.027	1.045	0.481
PM915Q01	1.647	4.314	1.247	3.150
PM915Q02	0.820	-1.280	0.918	-1.070
PM982Q01	1.212	0.770	1.012	0.132
PM982Q02	1.141	1.039	1.167	2.092
PM982Q03T	1.282	1.817	1.057	0.742
PM982Q04	0.902	-0.910	0.910	-1.379
PM992Q01	0.942	-0.231	0.914	-0.900
PM992Q02	0.804	-0.866	0.995	-0.008
PM992Q03	0.722	-0.818	0.810	-1.311

從表10.6可觀察到，只有6 道題目，其infit t考驗值達顯著水準，而且落在(-2, 2)區間之外，而其餘30 道題目則符合Rasch 模型。

10.9 我們該如何運用基於殘差的適合度統計量？

雖然在理論上，當我們想要用一個數學模型來描述一組資料，我們必須要檢查該組資料是否符合所採用的模型，然而，要詮釋基於殘差的適合度統計量卻有點複雜。以下讓我們來總結，在詮釋時哪些是可行的？哪些是不可行的？

檢查哪些題目是低適配的題目(即適合度均方值>1)，但不要刪除過度適配的題目(即適合度均方值<1)。
對於那些過度適配的題目，建議考慮該等題目的配分(權重)可以增加，關於這點，我們在討論部份給分的題目(partial credit items)和雙參數模型(two-parameter models)的章節時會做進一步說明。
當要對題目做比較保守的評估時，可以參考infit-t考驗值，但需要留意的是，如果樣本數很大時，其適合度t考驗值也會很大。
除了適合度統計量外，宜同時參考題目的其他統計量，尤其是點二系列的相關係數(point-biserial correlations)。

10.10 回家作業

請透過電腦模擬，產生一組符合Rasch模型人數為200位學生的題目作答資料，這200位學生的能力值是從N(0,1)的分佈隨機抽取，他們一共作答30道題目，題目的難度介於-2 到 2之間以等差數列的方式遞增，接著請用Rasch模型對該組資料進行校準，並計算基於殘差的適合度統計量。請報導outfit均方值的範圍為何？infit均方值的範圍為何？

References

Wright, Benjamin, and Geofferey Masters. 1982. Rating Scale Analysis. Book. Mesa Press Chicago.

Wu, Margaret, and Raymond J. Adams. 2013. “Properties of Rasch Residual Fit Statistics.” Journal of Applied Measurement 14 (4): 339–55.

第 10 章 基於殘差的題目適合度統計方法